Rectángulo Áureo

RECTÁNGULO ÁUREO

Un rectángulo cuyos lados están en una proporción igual a la razón áurea es llamado un rectángulo áureo. Este es un rectángulo muy especial como veremos. Los griegos lo consideraban de particular belleza y lo utilizaron asiduamente en su arquitectura. Al parecer a la mayoría de las personas también les parece más agradable a la vista un rectángulo con esas proporciones entre sus lados, inconscientemente se diseñan infinidad de cosas que resultan tener la forma de un rectángulo áureo. Un rectángulo se puede dividir en dos piezas: un cuadrado sobre el lado más corto y otro rectángulo.

Para una determinada proporción de los lados del rectángulo inicial, usando este procedimieto obtenemos un rectángulo similar al inicial.

  Es fácil construir un rectángulo áureo a partir de un segmento de recta inicial como se puede ver enseguida:

La proporción áurea puede expresarse de esta manera: Un segmento se dice que está dividido en su razón extrema y media cuando el total del segmento es a la parte mayor como la parte mayor a la menor. (Euclides)

Así podemos obtener el número áureo

                                                             

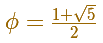
El hecho de que el proceso de obtención de rectángulos áureos es infinito sugiere que el número áureo es inconmensurable, es decir, que el número áureo es irracional.

Puesto que el lado de un pentágono regular y su diagonal están en proporción áurea y el pentágono y el pentagrama fueron los símbolos de los pitagóricos cabe la posibilidad de que se conociera que la diagonal de un pentágono y su lado son inconmensurables. Siendo éstos los primeros inconmensurables conocidos. Sin embargo, la primera demostración de la inconmensurabilidad de dos segmentos de la que tenemos constancia corresponde al lado y diagonal de un cuadrado (Euclides).

En la imagen anterior se puede mostrar el ejemplo de un rectángulo áureo realizado en el programa de AutoCAD elaborado con dos sencillas funciones de dicho programa: linea y circulo con los pasos explicados en clase, al final acotamos para ver las medidas y se vea que la proporción de sus lados es 1.618,

Por último les dejo el link del archivo mencionado anteriormente, espero sea de su agrado.

https://www.dropbox.com/s/2bftigwgekm465q/Drawing4.dwl?dl=0