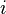Microsoft Excel

Microsoft Excel 

Microsoft Excel es una aplicación distribuida por Microsoft Office para hojas de cálculo. Este programa es desarrollado y distribuido por Microsoft, y es utilizado normalmente en tareas financieras y contable.  

 Entorno de Excel

 Barra de título 

Está situada en la parte superior de la ventana, y muestra el nombre del libro con el que estamos trabajando. También contiene hacia su derecha, los botones de minimizar, maximizar y cerrar ventana.

Barra de herramientas de acceso rápido 

Está situada de forma predeterminada en la parte superior izquierda de la ventana de la aplicación. Está formada por las herramientas que usemos más habitualmente. Así, podemos personalizarla y añadir o eliminar las herramientas que queramos: Guardar, Deshacer, Rehacer, Ortografía, Nuevo…

Cinta de opciones 

Está formada por un conjunto de fichas, las cuales tienen las distintas herramientas que necesitamos para trabajar con la hoja de cálculo. Cada ficha es específica y se relaciona con un tipo de actividad, elemento o acción, y algunas de ellas solo se muestran cuando hemos seleccionado un determinado elemento. 

 También podemos personalizar la cinta de opciones agregando fichas o grupos, y cambiando su nombre u orden. De manera predeterminada, el programa tiene las siguientes fichas: INICIO, INSERTAR, DISEÑO DE PÁGINA, FÓRMULAS, DATOS, REVISAR Y VISTA.

Para acceder a cada una de las fichas, solo tenemos que pinchar en la pestaña. O si queremos, también podemos utilizar los métodos abreviados del teclado. Para ello debemos utilizar la tecla correspondiente junto con la tecla ALT. Para saber cuáles son las teclas que se corresponden a cada ficha, tenemos que presionar la tecla ALT y ya nos saldrá encima de cada ficha la tecla correspondiente. Si queremos ocultar o mostrar el contenido de las fichas, debemos presionar a la vez las teclas CTRL y F1.

 Botón de Opciones de presentación de la cinta de opciones. Si pinchamos en él, se nos abre un desplegable con tres opciones:  Ocultar automáticamente la cinta de opciones Mostrar pestañas,  Mostrar pestañas y comandos.

 Barra de fórmulas

Está situada debajo de la cinta de opciones y muestra el contenido de la celda que está activa. Está dividida en tres sectores: el cuadro de nombres,los botones de insertar, aceptar y cancelar función,y el cuadro de fórmulas.

Menú archivo 

La primera ficha que tenemos, es la ficha Archivo. A diferencia de las demás, ésta es de color verde. Al pichar en ella, vamos a la Vista Backstage de Excel 2013. Aquí están las opciones de administración de archivos, éstas son: Nuevo, Abrir, Guardar, Guardar como, Imprimir, Compartir, Exportar, Cerrar, Cuenta y Opciones.

Cuando pinchemos en una de estas opciones, se nos abrirá en el panel de la derecha, las diferentes opciones que tiene cada una.  En Nuevo, podemos elegir entre un libro en blanco o las diferentes plantillas predefinidas, para que creemos un archivo nuevo. En Abrir, podemos abrir un archivo que tengamos guardado.  Desde Guardar y Guardar como, podemos guardar un archivo. Al pinchar en Imprimir, nos mostrará las opciones de impresión. En Compartir, nos muestra las opciones de cómo compartir nuestro archivo. Exportar, para poder cambiar el tipo de archivo. En Opciones, accederemos a las herramientas generales de configuración de Excel 2013, y a las diferentes opciones para personalizar la Cinta de opciones y la Barra de herramientas de acceso rápido. Como anclar archivos Si queremos tener un archivo a mano, podemos anclarlo a la lista de Libros recientes. Tenemos que pinchar sobre el archivo con el botón derecho del ratón, y pinchar en Anclar a.

La lista. 

En la lista, podemos anclar hasta 25 archivos, pero podemos elegir el número de archivos que queremos ver. 

Barra de estado

Se sitúa en la parte inferior de la ventana de la aplicación y es de color verde. En ella podemos ver el resultado de operaciones. A la izquierda, nos muestra la información del estado de la celda que tengamos seleccionada:  Listo, si no estamos haciendo nada  Introducir, si estamos escribiendo datos en una celda vacía Modificar, si estamos editando una celda. A la derecha del estado de la celda, tenemos los botones de vista, desde donde elegiremos como queremos ver la hoja de cálculo. Tenemos tres opciones:  Normal,  Diseño de página, Vista previa de salto de página 

En la parte derecha tenemos el Zoom. Si pinchamos en la barra de estado con el botón derecho del ratón, se nos abre el desplegable de Personalizar la Barra de estado, desde donde podemos activar o desactivar las distintas opciones de acuerdo a nuestras necesidades.

Algunas de las características que posee el programa Excel:

Celdas.- Esta es la principal forma de ingresar datos, emula directamente los libros de contabilidad.

Efectos.- Son procesos predefinidos en los que introducimos datos y se producen las sumas o movimientos de graficas automáticamente al existir modificaciones, podemos incluir imágenes que muestren los datos o aspectos directos de la información introducida.

Formatos.- Esta es una de las características que más destacan, pues pueden tener diversos formatos, cambiando desde alineación, hasta tipo y color de letras.

Gráficas.- Con el Excel, podemos utilizar gráficas que dan una idea visual de las estadísticas de los datos que estamos manejando.

Herramientas.- Las herramientas son pequeños procesos predefinidos, que modifican el denominado libro. Con estas se pueden dar efectos que se modifican según los usos que se le den.

Vínculos.- En las hojas de Excel, se pueden insertar vínculos, imágenes o directamente direcciones de internet que se abren automáticamente al hacer clic en el enlace.

Plantillas.- Cuenta con numerosas plantillas preestablecidas que facilitan la creación de diversos documentos como:

Agendas

Calendarios

Facturas

Horarios

Informes

Presupuestos etc.

Además de que el usuario puede crear sus propias plantillas personalizadas con las especificaciones que necesite.

Compatibilidad.- Este sistema comparte la denominada compatibilidad, que le permite abrir y editar documentos de este tipo realizadas con plataformas similares como son:

-Open office

-KOffice

-Star Office etc.

Evolución.- Este sistema se adapta a las necesidades, transformándose eventualmente mediante actualizaciones o nuevas versiones.

Así, cada nueva versión se encuentra mejor estructurada que la anterior, con más funciones y retirando funciones que resultan obsoletas.

Auto textos.- Esta es una de las funciones automáticas más utilizadas, y es cuando los usuarios ingresan datos iguales o similares en las casillas, y el programa los auto-detecta y los convierte en textos con formato y completándolos.

Herramientas.- Cuenta con diversas herramientas para con las que se realizan varias tareas, como autosuma y otras con las que se facilita hacer diversas operaciones dentro de las distintas celdas que componen la hoja de cálculo automatizando las operaciones evitando al usuario hacer cada operación por separado.

Difusión.- Por las distintas herramientas, la facilidad de manejo que posee y demás capacidades que tiene para realizar el trabajo, ha sido el programa de hoja de cálculo que en los últimos años ha tenido mayor difusión en el mundo.

Actividad 2.2

Dia de muertos

Actividad 4

Memorama Algebraico

Memorama algebraico from Edgar Mata

Material Didáctico: Memorama algebraico.

Materia: Álgebra Lineal.

Alumno: Santiago Jesús Torres Ontiveros.

Grupo y sección: 1° ''A''.

Profesor: Lic. Edgar Gerardo Mata.

Carrera: Procesos Industriales Área Manufactura.

Conceptos consultados tal y como vienen en biografía.

Término algebraico:  

Es una expresión algebraica que consta de un símbolo o de varios símbolos no separados entre sí por el signo + o -. Así, a - 3b; 2x + y.

Signo: 

Este indica si la propiedad es positiva o negativa. Todos los números enteros distintos de cero deben de llevar un signo.

Coeficiente: 

En el producto de dos factores, cualquiera de los factores es llamado coeficiente del otro factor.

Ejemplo 3a  el factor 3 es coeficiente del factor a e indica que el factor a se toma como sumando tres veces, ósea 3a= a+a+a.

Variable:

 Una letra o símbolo que representa cualquier elemento de un conjunto.

Exponente:

Número utilizado para indicar el número de veces que se utiliza un término como factor para multiplicarse por sí mismo. 

Monomio:

Es una expresión algebraica que consta de un solo término, Como 3a.

Binomio:

Es la suma de dos monomios o una expresión algebraica que consta de dos términos, como a+b.

Trinomio:

Es un polinomio que consta de tres términos, como a+b+c.

Polinomio:

Es una expresión algebraica que consta de más de un término como a+b, a+x-y.

Grado respecto a una variable:

El grado de un polinomio con una sola variable (como x) es el exponente más grande de la variable.

Ejemplo de polinomio con mas de tres términos:

abᶟ - 3ab² + ab + 5.

Grado Absoluto:
Es la suma de los exponentes de todas y cada una de sus variables.

Literales utilizadas como constantes:

Son las variables principales del abecedario por ejemplo a,b,c.

Estas toman un valor constante en una ecuación.

Concepto de expresión algebraica:

Es el resultado obtenido al aplicar sumas, restas, multiplicaciones, divisiones, potencia o tomar raíces de esta colección de variables o números reales, representación de un símbolo o de una operación algebraica.

Ejemplo de términos semejantes:

Los términos son semejantes cuando tienen el mismo valor literal. Por ejemplo: 7xy² +3xy-xy.

Ejemplo de término que contenga 3 variables y sea de grado absoluto igual a 6:

5n⁶ -n²-n.

Ejemplo de binomio:

x + y.

Ejemplo de término que contenga 3 variables y sea de grado 3 respecto a equis:

xᶟ - x² - x.

Ejemplo de término que contenga 3 variables y sea de grado 3 respecto a ye:

yᶟ + y² + y.

Ejemplo de trinomio:

a + b + c.

Definiciones personales de los conceptos anteriores:

Término algebraico:

Es una representación algebraica que consta de números y símbolos separados por su sigo + o -.

Signo:

Es aquel que nos indica si su posición es antes o después del cero, negativo o positivo.

Coeficiente:

Es su número de referencia que está antes de la variable, ya sea que no tenga, su valor es de uno.

Variable:

Ya sea esta letra o símbolo, es la que representa un elemento.

Exponente:

Es es número que se usa para saber a cuantas veces esta elevado nuestro elemento y se encuentra encima de este. 

Monomio:

Expresión algebraica que sólo tiene un término.

Binomio:

Conjunto de dos monomios o dos términos.

Trinomio:

Expresión algebraica compuesta por tres términos.

Polinomio:

Conjunto de elementos algebraicos que contienen dos o mas términos.

Grado respecto a una variable:

Es el exponente de mayor valor que se encuentra en un polinomio.

Ejemplo de polinomio con mas de tres variables:

x + xy + yx + y.

Grado absoluto:

Se le llama grado absoluto por que se realiza la suma de cada uno de los expontentes.

Literales utilizadas como constantes:

Son las principales letras del abecedario, (a. b, c) estas se representan como variables.

Concepto de expresión algebraica:

Es cuando  se lleva a cabo una operación de cualquier tipoy se representa su resultado obtenido.

Ejemplo de términos semejantes:

Los términos semejantes es cuando se repiten sus letras 3ab² + ab - 3.

Ejemplo de término que contenga 3 variables y sea de grado absoluto igual a 6:

x⁶  + x² + 2x².

Ejemplo de binomio:

a + b.

Ejemplo de término que contenga tres variables y sea de grado 3 respecto a x:

3xᶟ - x² - x.

Ejemplo de término que contenga tres variables y sea de grado 3 respecto a ye:

2yᶟ - y²  + y.

Ejemplo de trinomio:

x + xy + y.

Biografías utilizadas:

-Álgebra y Trigonometría con Geometría Analítica. Autor: Swokowski.

-Álgebra. Autor: CONAMAT

-Baldor, A. 1997. Álgebra. Publicaciones Culturales. México

Evidencias de la elaboración del memorama.

Elementos de Word

 Los diferentes elementos más importantes de la ventana de Word son:

Botón de office: Integra los comandos que se utilizan para crear, guardar, abrir e imprimir un documento, entre otras opciones.

Barra de título: Ubicada en la parte superior de la ventana, esta barra nos indica cual es la aplicación abierta (en este caso Microsoft Word) y el documento que está abierto. Por ejemplo, cada vez que abrimos Word en la barra de título aparecerá Documento1 – Microsoft Word.

Barra de menú: Debajo de la barra de título nos encontramos la barra de menús desde donde comandos de Word. La barra de menús tiene un comportamiento “inteligente”, que consiste básicamente, en mostrar sólo los comandos más importantes y los que el usuario va utilizando.

La barra de herramientas estándar: contiene iconos para ejecutar de forma inmediata algunos de los comandos más habituales (Guardar, Copiar, Pegar, etc.)

La barra de formato: contiene las operaciones más comunes sobre formatos, como poner en negrita, cursiva, elegir tipo de fuente, etc.

Barra de herramientas de acceso rápido:

Permite integrar los comandos de uso frecuente: Guardar, Abrir, Nuevo, Hacer, Deshacer, y otros, según el gusto del usuario, ya que se puede personalizar.

Personalizar: Podemos decidir qué iconos deben aparecer y cuales no en cada barra, es lo que se suele llamar “personalizar”. A lo largo de este curso verás imágenes con iconos que no están en las barras de tu ordenador.

 Panel de tareas: Este elemento no existía en versiones anteriores de Word. El panel de tareas es sensible al contexto, esto quiere decir que mostrará información diferente según lo que estemos haciendo en el momento de abrirlo

Barra de estado:
Presenta la información de lo que esta pasando con el programa y con el documento. La información que proporciona es el numero de la pagina que esta visualizando en pantalla, la línea y columna donde se encuentra el cursor, y el idioma que esta predeterminado en el programa para hacer la revisión ortográfica y gramatical.

Regla:
Es la guía situada en la parte superior y también en el lateral izquierdo del ambiente de trabajo, que te permite determinar, en centímetros, la ubicación del texto, dibujos, imágenes, tablas, etc.

Ventana del documento:
Es ahí donde se trabaja en el documento, que es el equivalente a la hoja de papel. En esta ventana aparece el punto de inserción, mejor conocido como cursor, el cual se va desplazando conforme vas tecleando el texto.

Barra de desplazamiento:
Te permiten mover el documento en la pantalla.

Botones de vista:
Permite visualizar el documento en distintos tipos de vista.

Zoom:
Permite ajustar el porcentaje de visualización del documento activo.

Actividad 3. Ejercicios resueltos

Se presentan los resultados de los problemas publicados anteriormente.

Actividad 3. Potencias y raíces de Números complejos.

Activity 3 de moivre theorem from Edgar Mata

Actividad 2. Números complejos resueltos

En base a la actividad publicada anteriormente.

Profesor, por favor, ¡explíqueme!

¿Por qué algunos universitarios aún tienen dependencia de los profesores? ¿Por qué ciertos alumnos siguen batallando con las matemáticas? ¿Tendrá algo que ver con su falta de interés? 

Si bien es cierto que este problema se tiene de ya hace tiempo, esto se fue agravando con el paso de los años por las distracciones que se interpusieron a la educación. Se dice que el uso excesivo de las tecnologías y sus aparatos, causan una deficiencia en la retención de información que se guarda en nuestro cerebro y esto tendría algo que ver del por qué se olvida esta rama tan importante de las matemáticas que es el álgebra.

Otra explicación que se le podría dar a estas preguntas, es que, los alumnos a nivel medio superior tienen cierta falta de interés en lo que es aprender, no extraen todos los conocimientos que deberían de las materias que se les imparte, algunos de ellos solo piensan en la calificación y no en el aprendizaje y esto los lleva a solo retener los conocimientos por cierto tiempo y después los olvidan. Y como resultado cuando cursan la universidad ya no recuerdan como emplear lo aprendido.

Ya que de parte del alumno se tiene cierto problema, también podría tener algo de influencia de parte del profesor, ya que, como se sabe no todos los profesores tiene la vocación de hacer que el alumno aprenda, sino simplemente cumplir con el trabajo y dar la clase por vista. Aunque esto no justifica al alumno ya que él, si tuviera interés buscaría aprender por su lado, pero si en ocasiones no aprende teniendo la información fácil y a su alcance, creo que menos si él tiene que buscarla. Por eso es que requieren de nuevo la explicación del tema para recordarlo y seguir con el aprendizaje.

Actividad 2. Números Complejos

Complex numbers from Matematica de Samos

Ejercicio 1 Resuelto.

Ejercicio 1 from Santiago Torres Ontiveros

Ejercicio 1.

Exercise 1 complex numbers operations from Matematica de Samos

¿Qué son los Fractales?

                                                
Es un objeto geométrico cuya estructura se repite a diferentes escalas. Es decir, por mucho que nos acerquemos o alejemos del objeto, observaremos siempre la misma estructura. De hecho, somos incapaces de afirmar a qué distancia nos encontramos del objecto, ya que siempre lo veremos de la misma forma.

El termino fractal (del Latín fractus) fue propuesto por el matemático Benoît Mandelbrot en 1975. En la naturaleza encontramos muchas estructuras con geometría fractal. Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el seno de la teoría de la medida.
Existen muchísimos fractales, ya que como veremos, son muy fáciles de construir. Los ejemplos más populares son el conjunto “Mandelbrot” o el triángulo “Sierpinski”. Este último se realiza de una forma muy sencilla: dibujamos un triángulo grande, colocamos otros tres triángulos en su interior a partir de sus esquinas, repetimos el último paso.

Como puede verse, la estrategia más sencilla para conseguir un fractal, es coger una figura y reproducirla en versiones más pequeñas. Sin embargo, se pueden conseguir objetos muchos más complejos.
El conjunto de Mandelbrot
Fue propuesto en los años setenta, pero no fue hasta una década más tarde cuando pudo representarse gráficamente con un ordenador. Este conjunto se define a partir de un número “c” cualquiera, que define la siguiente sucesión:

           

                                

Los conjuntos de Julia

Estos conjuntos, fruto de los trabajos de Pierre Fatou y Gaston Julia en los años 1920, surgen como resultado de la aplicación reiterada de funciones holomorfas .

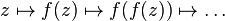
Analicemos el caso particular de funciones polinómicas de grado mayor que uno. Al aplicar sucesivas veces una función polinómica es muy posible que el resultado tienda a . Al conjunto de valores de  que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.

Estos conjuntos se representan mediante un algoritmo de tiempo de escape, en que cada pixel se colorea según el número de iteraciones necesarias para escapar. Suele usarse un color especial, a menudo el negro, para representar los puntos que no han escapado tras un número grande y prefijado de iteraciones.

                                    
La serie de figuras obtenidas se aproximaba a una figura límite que correspondía a lo que hoy llamamos conjunto fractal. Así, en 1904,Helge von Koch definió una curva con propiedades similares a la de Weierstrass: el copo de nieve de Koch. En 1915, Waclaw Sierpinski construyó sutriángulo y, un año después, su alfombra.

https://youtu.be/DK5Z709J2eo

Números imaginarios

Un número imaginario es un número complejo cuya parte real es igual a cero, por ejemplo:  es un número imaginario, así como  o  son también números imaginarios. En otras palabras, es un número de la forma:

Un número imaginario puede describirse como el producto de un número real por la unidad imaginaria i, en donde la letra i denota la raíz cuadrada de -1 :^1 2 3

Fue en el año 1777 cuando Leonhard Euler le dio a  el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que  era una especie de anfibio entre el ser y la nada.

Los números imaginarios se encuentran en el eje vertical del plano complejo, presentándolos como perpendiculares al eje real. Una manera de ver los números imaginarios es el considerar una recta numérica típica, que aumenta positivamente hacia la derecha y aumenta negativamente hacia la izquierda. 

Podemos entonces dibujar un eje de coordenadas vertical pasando por el 0 del eje horizontal, de modo que represente números imaginarios aumentando positivamente hacia arriba y negativamente hacia abajo. En esta representación, una multiplicación por –1 corresponde a una rotación de 180 grados sobre el origen.