¿Qué son los Fractales?

                                                
Es un objeto geométrico cuya estructura se repite a diferentes escalas. Es decir, por mucho que nos acerquemos o alejemos del objeto, observaremos siempre la misma estructura. De hecho, somos incapaces de afirmar a qué distancia nos encontramos del objecto, ya que siempre lo veremos de la misma forma.

El termino fractal (del Latín fractus) fue propuesto por el matemático Benoît Mandelbrot en 1975. En la naturaleza encontramos muchas estructuras con geometría fractal. Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el seno de la teoría de la medida.
Existen muchísimos fractales, ya que como veremos, son muy fáciles de construir. Los ejemplos más populares son el conjunto “Mandelbrot” o el triángulo “Sierpinski”. Este último se realiza de una forma muy sencilla: dibujamos un triángulo grande, colocamos otros tres triángulos en su interior a partir de sus esquinas, repetimos el último paso.

Como puede verse, la estrategia más sencilla para conseguir un fractal, es coger una figura y reproducirla en versiones más pequeñas. Sin embargo, se pueden conseguir objetos muchos más complejos.
El conjunto de Mandelbrot
Fue propuesto en los años setenta, pero no fue hasta una década más tarde cuando pudo representarse gráficamente con un ordenador. Este conjunto se define a partir de un número “c” cualquiera, que define la siguiente sucesión:

           

                                

Los conjuntos de Julia

Estos conjuntos, fruto de los trabajos de Pierre Fatou y Gaston Julia en los años 1920, surgen como resultado de la aplicación reiterada de funciones holomorfas .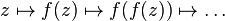

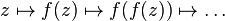Analicemos el caso particular de funciones polinómicas de grado mayor que uno. Al aplicar sucesivas veces una función polinómica es muy posible que el resultado tienda a . Al conjunto de valores de  que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.

Estos conjuntos se representan mediante un algoritmo de tiempo de escape, en que cada pixel se colorea según el número de iteraciones necesarias para escapar. Suele usarse un color especial, a menudo el negro, para representar los puntos que no han escapado tras un número grande y prefijado de iteraciones.

                                    
La serie de figuras obtenidas se aproximaba a una figura límite que correspondía a lo que hoy llamamos conjunto fractal. Así, en 1904,Helge von Koch definió una curva con propiedades similares a la de Weierstrass: el copo de nieve de Koch. En 1915, Waclaw Sierpinski construyó sutriángulo y, un año después, su alfombra.

https://youtu.be/DK5Z709J2eo