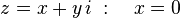En base a la actividad publicada anteriormente.
domingo, 27 de septiembre de 2015
Profesor, por favor, ¡explíqueme!
¿Por qué algunos universitarios aún tienen dependencia de los profesores? ¿Por qué ciertos alumnos siguen batallando con las matemáticas? ¿Tendrá algo que ver con su falta de interés?
Si bien es cierto que este problema se tiene de ya hace tiempo, esto se fue agravando con el paso de los años por las distracciones que se interpusieron a la educación. Se dice que el uso excesivo de las tecnologías y sus aparatos, causan una deficiencia en la retención de información que se guarda en nuestro cerebro y esto tendría algo que ver del por qué se olvida esta rama tan importante de las matemáticas que es el álgebra.
Ya que de parte del alumno se tiene cierto problema, también podría tener algo de influencia de parte del profesor, ya que, como se sabe no todos los profesores tiene la vocación de hacer que el alumno aprenda, sino simplemente cumplir con el trabajo y dar la clase por vista. Aunque esto no justifica al alumno ya que él, si tuviera interés buscaría aprender por su lado, pero si en ocasiones no aprende teniendo la información fácil y a su alcance, creo que menos si él tiene que buscarla. Por eso es que requieren de nuevo la explicación del tema para recordarlo y seguir con el aprendizaje.
sábado, 26 de septiembre de 2015
¿Qué son los Fractales?
Es un objeto geométrico cuya estructura se repite a diferentes escalas. Es decir, por mucho que nos acerquemos o alejemos del objeto, observaremos siempre la misma estructura. De hecho, somos incapaces de afirmar a qué distancia nos encontramos del objecto, ya que siempre lo veremos de la misma forma.
El termino fractal (del Latín fractus) fue propuesto por el matemático Benoît Mandelbrot en 1975. En la naturaleza encontramos muchas estructuras con geometría fractal. Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el seno de la teoría de la medida.
Existen muchísimos fractales, ya que como veremos, son muy fáciles de construir. Los ejemplos más populares son el conjunto “Mandelbrot” o el triángulo “Sierpinski”. Este último se realiza de una forma muy sencilla: dibujamos un triángulo grande, colocamos otros tres triángulos en su interior a partir de sus esquinas, repetimos el último paso.
El conjunto de Mandelbrot
Fue propuesto en los años setenta, pero no fue hasta una década más tarde cuando pudo representarse gráficamente con un ordenador. Este conjunto se define a partir de un número “c” cualquiera, que define la siguiente sucesión:


Los conjuntos de Julia
Estos conjuntos, fruto de los trabajos de Pierre Fatou y Gaston Julia en los años 1920, surgen como resultado de la aplicación reiterada de funciones holomorfas 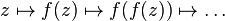 .
.
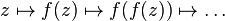 .
.
Analicemos el caso particular de funciones polinómicas de grado mayor que uno. Al aplicar sucesivas veces una función polinómica es muy posible que el resultado tienda a  . Al conjunto de valores de
. Al conjunto de valores de  que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.
que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.
 . Al conjunto de valores de
. Al conjunto de valores de  que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.
que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.
Estos conjuntos se representan mediante un algoritmo de tiempo de escape, en que cada pixel se colorea según el número de iteraciones necesarias para escapar. Suele usarse un color especial, a menudo el negro, para representar los puntos que no han escapado tras un número grande y prefijado de iteraciones.
La serie de figuras obtenidas se aproximaba a una figura límite que correspondía a lo que hoy llamamos conjunto fractal. Así, en 1904,Helge von Koch definió una curva con propiedades similares a la de Weierstrass: el copo de nieve de Koch. En 1915, Waclaw Sierpinski construyó sutriángulo y, un año después, su alfombra.

https://youtu.be/DK5Z709J2eo
Números imaginarios
Un número imaginario es un número complejo cuya parte real es igual a cero, por ejemplo:  es un número imaginario, así como
es un número imaginario, así como 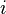 o
o  son también números imaginarios. En otras palabras, es un número de la forma:
son también números imaginarios. En otras palabras, es un número de la forma:
 es un número imaginario, así como
es un número imaginario, así como 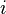 o
o  son también números imaginarios. En otras palabras, es un número de la forma:
son también números imaginarios. En otras palabras, es un número de la forma:
Un número imaginario puede describirse como el producto de un número real por la unidad imaginaria i, en donde la letra i denota la raíz cuadrada de -1 :1 2 3
Fue en el año 1777 cuando Leonhard Euler le dio a  el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que
el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que  era una especie de anfibio entre el ser y la nada.
era una especie de anfibio entre el ser y la nada.
 el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que
el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que  era una especie de anfibio entre el ser y la nada.
era una especie de anfibio entre el ser y la nada.
Los números imaginarios se encuentran en el eje
vertical del plano
complejo,
presentándolos como perpendiculares al
eje real. Una manera de ver los números imaginarios es el considerar una recta numérica típica,
que aumenta positivamente hacia la derecha y aumenta negativamente hacia la
izquierda.
Podemos entonces dibujar un eje de coordenadas vertical pasando por
el 0 del eje horizontal, de modo que represente números imaginarios aumentando
positivamente hacia arriba y negativamente hacia abajo. En esta representación,
una multiplicación por –1 corresponde a una rotación de
180 grados sobre el origen.
Números Irracionales
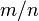 , donde
, donde  y
y  son enteros y
son enteros y  es diferente de cero. Es
cualquier número real que no es racional.
es diferente de cero. Es
cualquier número real que no es racional.
Los números irracionales son los elementos de la recta real
que no pueden expresarse mediante el cociente de dos enteros y se caracterizan
por poseer infinitas cifras decimales aperiódicas. De este modo, puede
definirse al número irracional como una fracción decimal aperiódica infinita.4
En general, toda expresión en números decimales es solo una aproximación en
números racionales al número irracional referido, por ejemplo, el número
racional 1,4142135 es solo una aproximación a 7 cifras decimales del número
irracional raíz cuadrada de 2, el cual posee infinitas cifras decimales no
periódicas.
Entonces, decimos con toda propiedad que el número raíz
cuadrada de dos es aproximadamente igual a 1,4142135 en 7 decimales, o bien es
igual a 1,4142135… donde los tres puntos hacen referencia a los infinitos
decimales que hacen falta y que jamás terminaríamos de escribir.
Debido a ello, los números irracionales más conocidos son identificados mediante símbolos especiales; los tres principales son los siguientes:
 (Número "pi" 3,14159...): razón entre la longitud de una circunferencia y su diámetro.
(Número "pi" 3,14159...): razón entre la longitud de una circunferencia y su diámetro.- e (Número "e" 2,7182...):
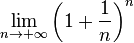
 (Número "áureo" 1,6180...):
(Número "áureo" 1,6180...): 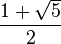
Los números racionales, son el conjunto de números
fraccionarios y números enteros representados por medio de fracciones. Este
conjunto está situado en la recta real numérica pero a diferencia de los números
naturales que son consecutivos, por ejemplo a 4 le sigue 5 y a este a su vez le
sigue el 6, y los números negativos cuya consecución se da así, a -9 le sigue
-8 y a este a su vez le sigue -7; no
poseen consecución pues entre cada número racional existen infinitos números
que solo podrían ser escritos durante toda la eternidad.
Todos los números fraccionarios son números racionales, y
sirven para representar medidas. Pues a veces es más conveniente expresar un
número de esta manera que convertirlo a decimal exacto o periódico, debido a la
gran cantidad de decimales.
Los números racionales limitados, cuya representación decimal
tiene un número determinado fijo de cifras, por ejemplo 1/8 es igual a 0,125.
Números Enteros
El conjunto de los números enteros está formado por los
naturales, sus opuestos (negativos) y el cero.
Enteros = {... −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}.
Dado que los enteros contienen los números enteros
positivos, se considera a los números naturales son un subconjunto de los
números enteros. Los enteros con la adición y la multiplicación forman una
estructura algebraica llamada anillo. También pueden ser considerados una
extensión de los números naturales y un subconjunto de los números racionales
(fracciones).
Los números enteros son subconjunto de los números racionales o
fracciones, puesto que cada número entero puede ser considerado como una
fracción cuyo denominador es el número uno.
Al igual que los números naturales, los números enteros
pueden sumarse, restarse, multiplicarse y dividirse, de forma similar a los
primeros. Sin embargo, en el caso de los enteros es necesario calcular también
el signo del resultado.
El orden numérico es el que da la idea de que un número es
mayor o menor que otro número, o que hay diferencia real entre dos números.
Ejemplo: el orden de los cursos de la educación primaria es (1º primero, 2º
segundo, 3º tercero, 4º cuarto, 5º quinto)
Propiedades de los números naturales
El conjunto de los números naturales se representa por IN y
corresponde al siguiente conjunto numérico:
IN = {1, 2, 3, 4, 5, 6, 7, ........}
Los números naturales son un conjunto cerrado para las
operaciones de la adición y la multiplicación, ya que al operar con cualquiera
de sus elementos, resulta siempre un número perteneciente a IN.
Ejemplo: 2 + 6 = 8, el 8 pertenece a IN.
5 · 3 = 15, el 15 pertenece a IN.
No ocurre lo mismo con las operaciones inversas, o sea, la
sustracción y la división. Ellas no son operaciones cerradas en IN.
Ejemplo: 3 - 5 = -2, y -2 no es un elemento de IN.
1 : 4 =
0,25; y 0,25 no es un elemento de IN.
En los números naturales se cumplen las siguientes
propiedades para la adición:
Conmutatividad: a + b = b + a, con a y b pertenecientes a IN
Esto se puede apreciar claramente, ya que 3 + 6 = 9, es lo
mismo que 6 + 3 = 9.
Asociatividad: (a + b) + c = a + (b + c), con a, b y c
pertenecientes a IN
Verifiquemos que (5 +
2) + 6 = 5 + (2 + 6). Resolvamos los paréntesis:
7 + 6 = 5 + 8
13 = 13
En los números naturales se cumplen las siguientes
propiedades para la multiplicación:
Conmutatividad: a · b = b · a, con a y b pertenecientes a IN
Esto se puede apreciar claramente, ya que 3 · 6 = 18, es lo
mismo que 6 · 3 = 18.
Asociatividad: (a + b) + c = a + (b + c), con a, b y c
pertenecientes a IN
Verifiquemos que (5 ·
2) · 6 = 5 · (2 · 6). Resolvamos los paréntesis:
10 · 6 = 5 · 12
60 = 60
Elemento Neutro: a · 1 = a, con a perteneciente a IN.
Todo elemento de IN multiplicado por 1, resulta el mismo
elemento. 5 · 1 = 5; 9 · 1 = 9 ...
Distributividad: a·(b + c) = a·b + a·c, con a, b y c
pertenecientes a IN.
Verifiquemos que
5·(3 + 6) = 5·3 + 5·6
5·9 = 15 + 30
45 = 45
Sistemas de numeración no posicional
Los sistemas de numeración pueden clasificarse en dos grupos: posicionales y no-posicionales:
En los sistemas no-posicionales los dígitos tienen el valor
del símbolo utilizado, no depende de la posición que ocupan en el número.
En los sistemas de numeración ponderados o posicionales el
valor de un dígito depende tanto del símbolo utilizado, como de la posición que
ése símbolo ocupa en el número.
Por ejemplo, el sistema de numeración egipcio es no
posicional, en cambio el babilónico es posicional. Las lenguas naturales poseen
sistemas de numeración posicionales basados en base 10 ó 20, a veces con
subsistemas de cinco elementos. Además, en algunas pocas lenguas los numerales
básicos a partir de cuatro tienen nombres basados en numerales más pequeños.
Sistemas de numeración no posicionales.
Estos son los más antiguos, se usaban por ejemplo los dedos
de la mano para representar la cantidad cinco y después se hablaba de cuántas
manos se tenía. También se sabe que se usaba cuerdas con nudos para representar
cantidad.
Al igual que otras civilizaciones mesoamericanas, los mayas
utilizaban un sistema de numeración de raíz mixta de base 20 (vigesimal).
También los mayas preclásicos desarrollaron independientemente el concepto de
cero (existen inscripciones datadas hacia el año 36 a. C. que así lo atestiguan).
Un sistema de numeración es posicional cuando el número
representado se calcula asignando a cada dígito un valor que depende
exclusivamente de cada símbolo y de su posición. Los sistemas más comunes, los
sistemas de numeración en base constante, son sistemas posicionales. En cambio,
otros sistemas como el romano o BCD no lo son.
En los sistemas no posicionales, los dígitos tienen el valor
del símbolo utilizado, que no depende de la posición que ocupan en el número. En
estos sistemas, aunque se prefería un orden de representación, los dígitos
podían aparecer en cualquier posición. Entre los sistemas de numeración no posicional
se encuentra el romano:
X = 10
lX = -1 + 10 = 9
XXX = 10+10+10 = 30
XC = 100-10 = 90
En todos los ejemplos la X vale siempre 10.
Así como el egipcio:
El sistema de numeración egipcio era decimal y no
posicional. Cada unidad se representaba con un trazo vertical; las decenas, con
un arco, y las centenas, millares, decenas de millar, centenas de millar y
millones, con un jeroglífico específico.
Observa los siguientes ejemplos y comprueba que el valor es
el mismo en ambos casos.
Origen De Los Números
La historia de nuestros números
es muy antigua, no sabemos con certeza hace
cuánto tiempo los humanos comenzaron a usarlos, lo que sí podemos asegurar es
que desde el principio el hombre necesitó palabras para expresar cantidades,
siempre con el uso de los dedos de las manos como origen y en los primeros
pueblos primitivos. En el cultivo de la tierra y en los negocios con animales,
empezó un sistema de conteos de los números, ya sea con marcas hecha en un
tronco, nudos, piedras entre otras alternativas.
Con el paso del tiempo
necesitaron representar números cada vez mayores y tuvieron que inventar
símbolos adecuados. Los primeros sistemas de numeración estaban basados en la
yuxtaposición, es decir, en ir colocando los símbolos uno a continuación de
otro. Los Romanos por ejemplo, empleaban un conjunto de siete símbolos. Los
Números son ideas de cantidad que se encuentran en nuestra mente, es la forma
como representamos o escribimos una idea de cantidad. Nuestro sistema de
numeración es decimal. Recibe este nombre por que emplea diez símbolos. Es un
sistema de numeración que no está basado en la yuxtaposición, sino que es
posicional. Poco a poco, el sistema decimal fue suplantando al sexagesimal en
la vida corriente, per en los cálculos matemáticos de sacerdotes y sabios el
sistema sexagesimal siguió manteniéndose como indispensable para verificar
cálculos complicados, a la vez que se convertía en una especie de numeración
secreta.
Sin embargo, se encontraron con
números que era imposible transcribir con dicho sistema, el primero de los
cuales era 1/7; es imposible expresar la séptima parte de algo mediante
fracciones sexagesimales, pues se necesita una serie interminable: 1/7 = 8/60 +
34/3.600 + 17/216.000 + ... que los escribas anotaban como 8,34,17.
Esta irreductibilidad del número
7 hizo que lo consideraran de mal agüero y lo atribuyeran a los demonios
divinos, los cuales eran siete veces siete, es decir, totalmente irreductubles.
De aquí se deducía que el más prudente era no emprender ningún trabajo en los
días 7, 14 y 28 de cada mes. Ese fue el origen de la semana, y si bien el
Génesis y demás libros sagrados de los hebreos hicieron desaparecer el sentido
maléfico del siete, todavía lo sacralizaron más.
El sistema romano todavía es
utilizado, claro que en las fechas de monumentos, para escribir en algunos
textos los siglos, etc. El sistema de numeración actual fue inventado por los
Hindúes en el siglo II. Los Árabes los introdujeron en Europa a través de
España y desde allí se extendió por todo el mundo, ya que permitía operar con
grandes cifras de un modo muy sencillo. Entre los griegos y romanos, por
ejemplo, realizar una división o una multiplicación medianamente complicadas
requería años y años de estudios de matemáticas. Con el hallazgo de los
hindúes, cualquier niño puede aprender en el colegio las reglas básicas de la
aritmética.
Existe toda una teoría de los
números, que clasifica a los números en:
-Números naturales.
-Número primo.
-Números perfectos.
-Números enteros.
-Números pares.
-Números impares
-Números racionales
-Números reales.
-Números irracionales.
-Números algebraicos.
-Números trascendentes
-Números hiperreales.
-Números complejos.
-Cuaterniones.
-Números infinitos.
-Números negativos.
- Números fundamentales: π y e.
Las grandes civilizaciones de la
Antigüedad se distinguieron por un importante desarrollo de la aritmética y la
geometría.
Con la clasificación de los
números, surge otro problema natural más práctico, pero que condiciona todo lo
que se va a hacer con ellos: la manera de escribirlos. El sistema que se ha
impuesto universalmente es la numeración posicional, gracias al invento del
cero, con una base constante.
domingo, 20 de septiembre de 2015
Componentes de una Computadora.
Componentes de una Computadora
Primeramente, ¿Que es una computadora?
Es un sistema informático compuesto por varios componentes electrónicos que trabajan en conjunto para proporcionar datos de salida procesados. Estos componentes conforman el llamado hardware, y son los encargados de procesar todas las instrucciones que proporciona el software con el cual está cargada la computadora.
¿Cuales son sus componentes?
Unidad de sistema o gabinete:
La unidad del sistema o gabinete es el núcleo de un sistema informático. Normalmente, se trata de una caja rectangular. En el interior de esta caja se encuentran muchos componentes electrónicos que procesan información. El más importante de estos componentes es la CPU (unidad central de procesamiento), o microprocesador, que funciona como "cerebro" de la computadora.
Memoria RAM:
Es aquella que almacena temporalmente la información utilizada por la CPU mientras la computadora está siendo usada. La información almacenada en la memoria RAM es borrada cuando la computadora se apaga.
Unidades de CD, DVD y Blu-Ray
:todos las computadoras actuales están equipados con una unidad de CD o DVD, normalmente localizada en la parte frontal de la unidad de sistema, las unidades ópticas utilizan lásers para leer y escribir datos de un CD, DVD o Blu-Ray. Si tiene una unidad de disco grabable, puede guardar copias de los archivos en soportes ópticos vírgenes. También puede usar la unidad de CD para reproducir CDs de música en la computadora.
Las unidades de DVD pueden hacer todo lo que las unidades de CD hacen y, además de eso, pueden leer DVDs. Si tiene una unidad de DVD, puede ver películas en la computadora. En la actualidad todas las unidades de DVD pueden grabar datos en DVDs vírgenes de CD, DVD y Blu-Ray.
Mouse (Ratón):
El mouse es un pequeño dispositivo utilizando para apuntar y seleccionar ítems. A pesar de que los mouses tengan varias formas, el mouse típico tiene un aspecto que se parece a un ratón, de ahí su nombre. Es pequeño, redondeado y está conectado a la unidad de sistema por un cable. Algunos mouses más modernos son inalámbricos.
Teclado:
Es principalmente utilizado para escribir textos en la computadora. Tal como el teclado de una máquina de escribir, el teclado de la computadora tiene teclas con letras y números, pero también posee teclas especiales:
Las teclas de función, localizadas en la línea superior, efectúan funciones diferentes dependiendo del modo en el que son utilizadas.
El teclado numérico, localizado en el lado derecho de la mayor parte de los teclados, permite introducir números rápidamente.
Las teclas de navegación, tales como las teclas de flecha, permiten cambiar el posicionamiento en un documento o página web.
Monitor:
Este presenta información en forma visual, utilizando texto y gráficos. La parte del monitor que presenta la información es llamada pantalla. Tal como la pantalla de un televisor, la de una computadora puede mostrar imágenes fijas o en movimiento.
Impresora:
Una impresora transfiere datos de la computadora al papel. No es necesario tener una impresora para poder usar la computadora, pero si tienes una, podrás imprimir mensajes de correo electrónico, tarjetas, invitaciones, anuncios y cualquier otro material. Muchas personas también aprovechan la posibilidad de poder imprimir fotos en casa.
Altavoces o Parlantes:
Los parlantes son utilizados para reproducir sonidos. Los parlantes pueden estar integrados a la unidad de sistema o conectados a esta por medio de cables. Los parlantes permiten escuchar música y los efectos de sonidos producidos por la computadora.
Estos componentes van cambiando con el paso del tiempo de de las tecnologías que van modernizando sus elementos en una computadora.
Suscribirse a:
Comentarios (Atom)