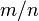, donde 
y 
son enteros y es diferente de cero. Es
cualquier número real que no es racional.
Los números irracionales son los elementos de la recta real
que no pueden expresarse mediante el cociente de dos enteros y se caracterizan
por poseer infinitas cifras decimales aperiódicas. De este modo, puede
definirse al número irracional como una fracción decimal aperiódica infinita.4
En general, toda expresión en números decimales es solo una aproximación en
números racionales al número irracional referido, por ejemplo, el número
racional 1,4142135 es solo una aproximación a 7 cifras decimales del número
irracional raíz cuadrada de 2, el cual posee infinitas cifras decimales no
periódicas.
Entonces, decimos con toda propiedad que el número raíz
cuadrada de dos es aproximadamente igual a 1,4142135 en 7 decimales, o bien es
igual a 1,4142135… donde los tres puntos hacen referencia a los infinitos
decimales que hacen falta y que jamás terminaríamos de escribir.
Debido a ello, los números irracionales más conocidos son identificados mediante símbolos especiales; los tres principales son los siguientes:
(Número "pi" 3,14159...): razón entre la longitud de una circunferencia y su diámetro.- e (Número "e" 2,7182...):
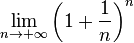
(Número "áureo" 1,6180...):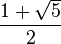 
No hay comentarios.:
Publicar un comentario